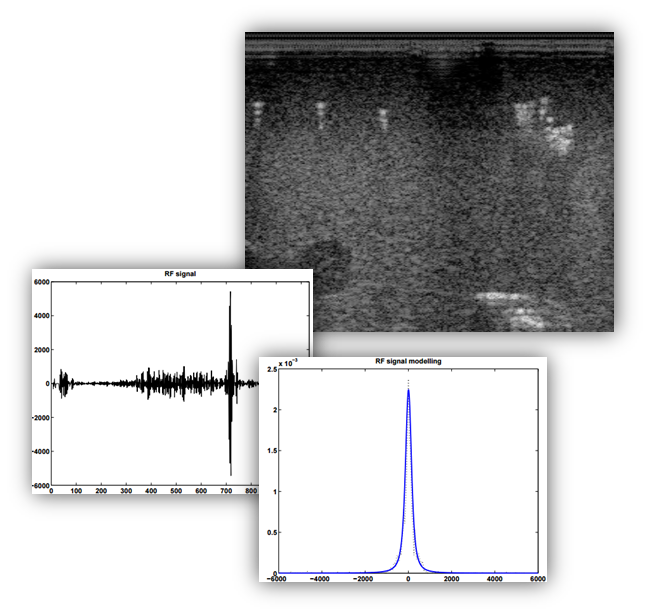
Research activities at SPL explore the statistical properties of linear time-frequency analysis methods, such as the short-time Fourier transform and multiresolution wavelet decompositions, towards designing efficient signal processing techniques, which are adapted to the inherent information content of the acquired signals. More specifically, our work demonstrates that the time-frequency decompositions of various distinct real world signals exhibit highly non-Gaussian statistics, which are best described by heavy-tailed distributions, and specifically the family of alpha-stable models. Statistical modelling of the available information is exploited to design optimal non-linear and Bayesian techniques for data processing. The adopted approach is unique in that it relates the optimal non-linearity to the degree of non-Gaussianity of the data. Such a methodology is applied to a wide range of applications, including medical and SAR image denoising and autofocusing, multiresolution data compression, blind watermark detection, texture image retrieval, and classification of underwater acoustic signals.
